세상에서 가장 어려운 문제? 리만가설

오늘은 리만 가설에 대해 포스팅 해보자.

하버드 대학의 수학자들이 '클레이 수학연구소' 라는 단체를 만들어 2000년에 "21세기 수학계기여할 수 있는 7가지 문제" 를 발표했는데, 한 문제당 100만 달러의 상금, 무려 10억의 상금이 걸려있는 문제들이다.

이중 증명된 것은 푸앵카레 추측으로, 7대 난제 모두 나중에 한번씩 포스팅해 보도록 하자

그럼 리만 가설이 뭘까?

그 문제는 다음과 같다 

리만 제타 함수 ζ(s)=0을 만족하는 모든 자명하지 않은 근의 실수부는 1/2 이다.

 

 

말이 어렵지만 그렇게 난해할만큼 어렵진 않다. 고등학생도 이해할 만큼 간단하게 설명해보자.

 

리만 제타 함수란, 실수부가 1보다 큰 복소수 s에 대하여 다음을 의미한다.

 

 

아니? 어떻게 복소수가 지수 값을 가질 수 있죠? 가 궁금하다면 다음 포스팅을 참고 하자 -> http://formath.tistory.com/3

 

어쨌든 리만 제타함수를 이해해보면 그렇게 어렵지만은 않아보인다.

 

리만 제타함수의 정의역을 복소평면 전체로 확장할 수 있는데확장된 리만 제타함수는 다음과 같다

 

 

참고로 이 식에 사용된 감마함수는 팩토리얼의 정의역을 해석적 확장을 통해 복소수 전체 범위로 확장한 것으로 다음 포스팅을 참고할 것 -> http://formath.tistory.com/8

 

감마함수의 정의를 안다면 치환적분을 통해 이 식이 제타함수와 동치라는 것을 고등학교 과정 내에서 충분히 밝힐 수 있다. 혹시 심심하면 해봐도 괜찮다.

 

또한 복소적분과 경로적분, 자이함수(또는 크시함수 : Xi function)가 1/2 에 대해 대칭임, 또 감마함수에 관한 반사공식을 이용하여 제타함수를 다음과 같은 식으로 변형할 수 있다. (과정이 어렵고 복잡하며, 과도한 선행지식을 요하므로 생략한다.)

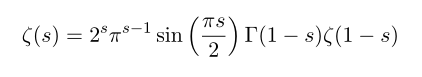
(원래는 그 과정을 다 적으려 했으나 쓰고보니 괜히 어렵게 느껴질 것 같아서 그만 뒀다. 혹시나 나중에 기회가 되면 포스팅을 해보자.)

 

이때 sin (pi s/2)=0 을 만족하는 영점을 제타함수의 자명한 근이라고 말한다. 이때 감마함수는 음의 정수에 대해 값이 존재하지 않으므로 감마함수 에 대입되는 값이 양의 정수가 되도록 하는 s 값은 음의 짝수 뿐이므로, 제타함수의 자명한(trivial) 근은 음의 짝수 뿐이다.

 

그러나 자명한 근이 제타함수의 유일한 근이 아니고, 정수범위 밖에 허수부가 0이 아닌 복소수의 경우에도 무수히 많은 근이 있는 것으로 알려져 있는데 이러한 근 들을 비-자명한 근이라고 말한다.

 

리만은 자신의 논문 " 주어진 수 보다 작은 소수의 개수에 관하여" 라는 논문에서 이 비자명한 근들의 모든 실수부가 1/2 인 것으로 예상했으나, 그에 관한 증명은 기록되지 않았기 때문에 가설이라고 이름이 붙었으며 당시 가설이 제시된 후 지금까지도 증명되지 않았기 때문에 수학 7대 난제로 불리게 된 것이다.

 

이 가설이 제시된 리만의 논문은 겨우 8~9페이지에 불과한데, 그 얼마 안되는 페이지를 가지고 현재까지도 해석적 정수론의 기반이 된 다양한 기법들이 제시되어있다.

 

리만은 이 가설을 제시할 당시 자명하지 않은 4개의 근을 직접 계산하는데, 그 점들을 복소평면에 나열했을 때 모두 일직선상에 있었고, 그 일직선이 바로 실수부가 1/2인 직선이었다. 이를 보고 다른 모든 제로점들이 실수부가 1/2 이 아닐까 라고 추측한 것이 리만 가설이다.

 

리만가설이 중요한 이유는 정수론에서 가장 중요하다고 볼 수 있는 소수와 관련이 있다는 점인데, x보다 작은 소수의 갯수를 나타내는를 파이를 통해 표현한다. 이를 소수 계량 함수라고 부른다.

 

 

물론 원주율과는 관련이 없다. 그냥 기호를 파이를 썼을 뿐이다.

 

카를 프리드리히 가우스와 아드리앵마리 르장드르는, 소수 계량 함수가 어떤 특정한 함수에 근접한다는 것을 추측했는데, 이는 다음과 같다.

 

 

이렇듯 소수의 갯수가 x/ln(x) 에 근접한다는 추측을 소수 정리라고 하는데, 이는 1896년에 리만 제타함수의 성질을 이용하여 증명되었다.

 

재밌는 사실은 소수 계량함수가 리만 제타 함수를 통해서 더 엄밀하게 함수가 정의될 수 있다.

 

현재까지 증명된 바로는 소수 계량 함수가 x/ln(x) 에 근접한다는 사실만 알지 소수사이의 정확한 간격은 알 수 없다. 만약 리만가설이 증명된다면, 두 함수사이의 오차를 더 좁힐 수 있으며, 소수사이의 간격이 어느정도인지 더 엄밀하게 알아낼 수 있다고 한다.

 

리만은 본인에 논문에서 리만가설의 증명이 그렇게 중요하지 않아서 넘어간다 라고 적어놨는데, 실제로 본인 논문의 주제는 제타함수에 관한 분석이 아니라 소수의 개수에 관한 것이었기 때문에 가설의 증명은 본인에게 있어서 그닥 중요하지 않았을 것으로 보인다. 해석적 정수론의 아버지라고 불릴만한 리만에게는 정말로 별로 안어려워서 안적고 대충 넘긴걸지도 모르겠다.